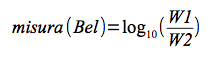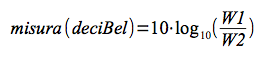MATH4ANALOG – Seconda parte

E adesso iniziamo a introdurre qualche argomento “succoso”.

Di Domenico Nocera

Logaritmi.

Il logaritmo è uno strumento matematico necessario quando si vuole affrontare il problema di misurare scale e sequenze che non hanno un andamento costante, e che quindi ci portano costantemente a lavorare con valori o molto piccoli o molto grandi. Avete fatto caso alla suddivisione in dodici semitoni delle ottave musicali del pianoforte raffigurato nella prima parte? Noterete che la differenza fra le frequenze di due tasti successivi aumenta man mano che ci spostiamo a destra (verso frequenze più alte). Eppure in questo caso parliamo di “temperamento equabile”, cioè i 12 semitoni dividono in modo uguale l’ottava. Uguali? Ma come? Ma no, non sono uguali!!! Vediamo di capirci qualcosa.

Nel mondo percettivo (vedi parte prima) la differenza di altezza (o tono, o pitch) fra un suono A con una frequenza di 100 Hertz e un suono B con una frequenza di 200 Hertz è molto inferiore alla differenza percepita fra due suoni B e C di frequenza 15600 e 15700, eppure la differenza numerica è uguale in entrambi i casi (100 Hertz).

Questo è dovuto alla quantità di energia trasportata da un’onda. Mettiamola così: alle basse frequenza, sede delle onde più potenti che devono portare con sé più energia a causa della maggiore lunghezza d’onda, ci vuole molta più “diversità” fra le onde per percepirle davvero diverse; alle alte frequenza, sede dei suoni acuti, già un piccolo spostamento di frequenza comporta un grande salto percettivo (riguardate di nuovo la figura del pianoforte).

Il Logaritmo per la scala delle Frequenze

Dunque il logaritmo ci viene in aiuto, perché ci permette di trattare distanze fra frequenze e fra intensità in una maniera relativa, e non assoluta.

Il logaritmo in base 10 di un numero X è l’esponente da dare a 10 per ottenere X. Esempio: se X è 1000 il logaritmo in base 10 di 1000 è 3, perché 10 elevato alla potenza di 3 fa 1000; il logaritmo in base 10 di 1000000 è 6, ecc…

Definizione formale di logaritmo: il logaritmo in base a di b è uguale all’esponente da dare ad a per ottenere b. Esempio: il logaritmo in base 2 di 8 è 3.

Ecco che su una scala logaritmica la “distanza” fra 1000 (il suo log in base 10 è 3) e 100000 (il suo log è 5) è la stessa che c’è fra 10 (il log è 1) e 1000 (il log è 3). In pratica vediamo a come radice L- esima di b:

Il gioco funziona grazie alla proprietà delle potenze che dice che il prodotto di potenze con la stessa base è la somma degli esponenti (sempre con stessa base) per cui trasformiamo grandissime (o piccolissime) distanze relative in numeri più gestibili perché ci concentriamo sugli esponenti di una base fissata (in questo caso 10).

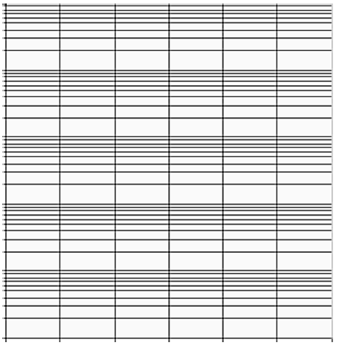
Questo è un pezzo di carta “semi-logaritmica” che ci permette di dare valori linearmente crescenti sull’asse orizzontale, e logaritmicamente crescenti sull’asse verticale. É utile per tracciare grafici logaritmici che per dare un senso al loro andamento devono obbligatoriamente “distorcere” l’andamento lineare.

Ciò che diventa importante in una scala logaritmica non è più la differenza (distanza) assoluta fra i valori, ma il rapporto fra i valori: 1000/10 = 354/3.54 = 100000/1000 = 100 (cioè 10 alla potenza di 2). (provate a posizionare questi valori sulla scala in figura sopra, collocando sull’asse verticale prima il numero 3.54 poi il numero 10, poi 1000 e 100000).

Tornando alle nostre frequenze, utilizzando la scala di un pianoforte o di una tastiera, la differenza di frequenza che c’è fra due DO successivi è… non si sa! Dipende da quali DO scegliete, se giù a sinistra dove le frequenza sono più basse o su a destra dove sono più alte. Quello però che sapete di sicuro è che il rapporto fra le frequenze di due note qualsiasi che siano distanti fra loro un’ottava musicale è di 1 a 2. Cioè ogni volta che saltate in su di un ottava da una nota alla sua gemella più alta, state raddoppiando la frequenza di quel suono, mentre la dimezzate se scendete invece di salire. Questo è un concetto logaritmico.

Per tornare alla suddivisione dell’ottava in 12 “parti uguali”, possiamo ora affermare che sono “logaritmicamente uguali” e non linearmente uguali! E infatti il temperamento equabile che tutti accettiamo ormai come assodato da oltre 500 anni, stabilisce che il rapporto fra le frequenze di due semitoni successivi sia di 1,0594631 : 1, e come Esercizio 2 vi lasciamo il compito di capire – o quantomeno di intuire – da dove salti fuori questo strano e complicato rapporto, ricordando che il rapporto fra due note che distano un’ottava è di 2:1.

Il Logaritmo per la scala delle Intensità

Abbiamo lo stesso problema (numeri molto grandi e molto piccoli, non-linearità delle misurazioni) quando vogliamo misurare delle intensità sonore, perché ovviamente queste dipenderanno dall’ascoltatore e dalla sua posizione nello spazio, o dagli apparecchi che riprendono o emettono il suono e dalle loro caratteristiche. Difficile dire “questo è un suono di potenza 34”, se un altro ascoltatore a 50 metri da me dirà che “è un suono di potenza 20”, perché la differenza di posizione implica che ad ascoltatori diversi arriveranno pressioni sonore diverse. E dunque quanto misura questo suono?

Per risolvere la questione dovremo abbandonare il tentativo di creare una scala lineare e assoluta lasciando solo agli speaker (cioè agli unici dispositivi che nella catena audio producono pressione acustica, utilizzando una corrente elettrica) la possibilità di misurare quanta forza mettono nel riprodurre un determinato segnale sonoro. In questo caso potremo parlare di potenza motrice espressa in Watt, che ci darà una valutazione della quantità di pressione prodotta dall’altoparlante, e che sarà di andamento lineare, in una scala che va da zero (spento) a un massimo X.

Se vogliamo invece parlare di percezione, dobbiamo tornare a una valutazione logaritmica dei segnali, che tengano sempre conto di un rapporto, e non una differenza, fra il segnale audio in oggetto e un livello di riferimento. Anche qui dunque useremo una scala logaritmica, che investiga sui rapporti e non sulle differenze. Stavolta, come preannunciato, useremo una nuova unità di misura, il Bel.

Il Bel è un’unità di misura per rapporti. Il rapporto espresso in Bel fra due quantità omogenee, W1 e W2 si definisce come:

e, per essere espresso in deciBel, deve essere moltiplicato per 10 (Il deciBel è la decima parte di un Bel):

Esempio: il rapporto fra le precipitazioni di Marzo (95 mm) e quelle di Febbraio (19 mm) è di 5:1. Possiamo dire che da Febbraio a Marzo c’è stato un incremento di cinque volte, o del 500%, o ancora possiamo misurare il rapporto e dire che c’è stato un “guadagno” di 6,9 dB, perchè il logaritmo in base 10 di 5 è circa 0,69.

Considerando che la minima pressione che noi umani riusciamo a decifrare come suono sulla terra (in camera anecoica) è di 20 microPascal (a questo livello di pressione urtano le molecole dell’aria sul nostro timpano), proprio a 20 microPascal ci mettiamo il nostro punto di riferimento (Wbase) e chiamiamo poi Wtest la pressione del suono di cui vogliamo misurare in modo logaritmico l’intensità.

Un suono ci risulta udibile se esercita sulle nostre orecchie una pressione di almeno 20 microPascal. Sopra i 200 Pascal rischia di romperci i timpani. E se in termini di pressione riusciamo a valutare un livello sonoro in un punto di rilevazione (ascoltatore, microfono), da questo dato tuttavia non otteniamo nessuna informazione sull’impronta pressoria (univoca!) del suono cosi com’è finché

attraversa la catena di generazione e riproduzione, prima di giungere all’impianto di diffusione. Dovremo usare una scala logaritmica (Bel, deciBel) per misurare le intensità sonore rispetto (in rapporto) a un punto minimo dichiarato equivalente al silenzio (Wbase=20 microPascal).

Definiamo il livello acustico L di un segnale di potenza Wtest misurato in Bel rispetto a un segnale base di potenza Wbase:

Decisa dunque la soglia inferiore (Wbase) a 20 microPascal, il livello del segnale audio (Wtest) in un normale giorno di traffico passeggiando per strada si aggirerà sugli 0,2 Pascal, per cui Wtest/Wbase ci da’ 100000000. Il logaritmo in base 10 di 100000000 è 8, dunque al segnale con potenza Wtest attribuiamo un’intensità (ma possiamo già chiamarlo guadagno rispetto a Wbase) che dichiariamo essere di 8 Bel, oppure 80 deciBel.

La soglia del dolore è situata intorno ai 200 Pascal, fra i 135 e i 140 deciBel. Un buono studio di registrazione dovrebbe garantire un rumore di fondo inferiore agli 0,2 millesimi di Pascal, cioè sotto i 30 dB.

N.B. In realtà poi nella formula di definizione dell’intensità acustica dovremo applicare nel reale utilizzo qualche correzione perché andrà tenuto conto che la potenza percepita sarà sempre in relazione con la superficie su cui impatta l’onda sonora (W/m2).

Con lo stesso ragionamento appena fatto per la soglia di udibilità umana, si può comprendere la necessità di misurare le intensità in uscita da un dispositivo (amplificatore, compressore, effetto,…) rispetto all’intensità del suono che vi era entrato per essere processato. La differenza fra i due segnali è il guadagno del dispositivo (Gain). Dunque d’ora in poi tutte le volte che misureremo in deciBel un segnale, sapremo che stiamo in effetti valutando il rapporto i livelli di un segnale prima e dopo un determinato punto della catena. Il fader di una traccia di un mixer a 0 dB indica che stiamo trasmettendo in uscita al master la stessa quantità di segnale che in quella traccia abbiamo immesso.

Esercizio 3: di quanto (di quante volte) amplifichiamo un segnale se gli applichiamo un guadagno di 1 dB? E di quanto diminuiamo la sua intensità se applichiamo un guadagno (negativo) di -5 dB?

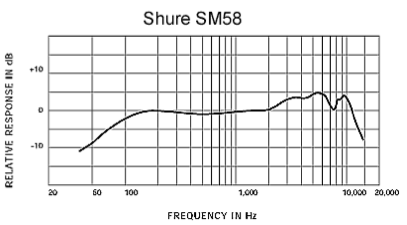
Un classico esempio di utilizzo di un grafico semi-logaritmico è quello che ci indica la cosiddetta risposta in frequenza di un dispositivo, in questo caso del celebre microfono Shure SM58. La risposta in frequenza ci dice come interviene il dispositivo sul segnale in ingresso, e come lo modifica in uscita. Quello che ci interessa graficare

è se, e quanto, accentua (boost) o affievolisce (cut) il segnale in corrispondenza di determinate frequenze. Il grafico in figura ci dice che l’SM58 riesce a trasferire inalterate le pressioni sonore che lo colpiscono con una frequenza di circa 200 Hz (dB=0), mentre opererà una amplificazione (guadagno, gain) di circa 5 dB ai suoni con frequenze fra i 4 e i 5 kHz. Sopra i 15 kHz e sotto i 50 questo microfono invece diventa un po’ “duro d’orecchi”, in quanto applicherà a causa delle sue caratteristiche interne dei guadagni negativi inferiori ai -10dB ai suoni con quelle frequenze. Microfoni invece specializzati sulle basse frequenze (per la cassa della batteria ad esempio) avranno risposte più “fedeli” e quindi più vicine allo zero nella zona delle basse frequenze, mentre saranno alquanto “sordi” nella parte destra del grafico; ecc..